Abstract
The formation and stability of social hierarchies is a question of general relevance. Here, we propose a simple generalized theoretical model for establishing social hierarchy via pair-wise interactions between individuals and investigate its stability. In each interaction or fight, the probability of “winning” depends solely on the relative societal status of the participants, and the winner has a gain of status whereas there is an equal loss to the loser. The interactions are characterized by two parameters. The first parameter represents how much can be lost, and the second parameter represents the degree to which even a small difference of status can guarantee a win for the higher-status individual. Depending on the parameters, the resulting status distributions reach either a continuous unimodal form or lead to a totalitarian end state with one high-status individual and all other individuals having status approaching zero. However, we find that in the latter case long-lived intermediary distributions often exist, which can give the illusion of a stable society. As we show, our model allows us to make predictions consistent with animal interaction data and their evolution over a number of years. Moreover, by implementing a simple, but realistic rule that restricts interactions to sufficiently similar-status individuals, the stable or long-lived distributions acquire high-status structure corresponding to a distinct high-status class. Using household income as a proxy for societal status in human societies, we find agreement over their entire range from the low-to-middle-status parts to the characteristic high-status “tail”. We discuss how the model provides a conceptual framework for understanding the origin of social hierarchy and the factors which lead to the preservation or deterioration of the societal structure.
1 Introduction
Animals, including humans, form social hierarchies [1–5]. How these hierarchies form and what makes them remain stable over time is a central question across many different fields. In the humanities, social and political theorists have studied the origin of class structures and the conditions under which these structures are preserved or change [6–9]. Archaeologists and other researchers from diverse fields study the factors that lead to the collapse of civilizations [10, 11]. Anthropological research has focused on the roles of norms, sanctions, and cooperative behaviour in creating and maintaining hierarchy [12–14]. In the biological sciences, researchers have questioned whether hierarchy emerges primarily from differences in intrinsic qualities of individuals (e.g. physical strength, intelligence, or aggressive tendency) or as a self-organizing process in which a hierarchy arises as a result of many interactions between the members of the society [15–18].
From a high-level perspective, a fundamental question arises: Can a stable or long-lived hierarchical structure occur entirely by self-organization, based solely on inter-individual interactions, modeled as independent pair-wise “fights”? And, if so, what are the typical structures of hierarchy, and what are the characteristic times of formation and evolution of the said structures?
“Winner-loser” models are a class of mathematical models that have been used to study the self-organization of social hierarchy in biology [18–29] and economics [30–34]. In these models, individuals are characterized by a property, such as “strength”, “resource holding potential”, or “wealth”, that determines the individual’s position in society (in the following, we use “strength” as a generic term for this property). Pairs of individuals come into contact and engage in an interaction (or “fight”). The fight has a winner and a loser, where the winner experiences a gain in strength, and the loser loses strength. The models have two basic rules: one that determines who wins in a given fight, and another that determines the amount of strength gained or lost in a fight. The distribution of strength, which changes as individuals interact with each other, represents the societal structure resulting from the model. While stable societal structures have been analyzed in previous studies of winner-loser models, the time evolution and intermediary, potentially long-lived societal structures have been mostly neglected. Here, we aim to close this crucial knowledge gap.
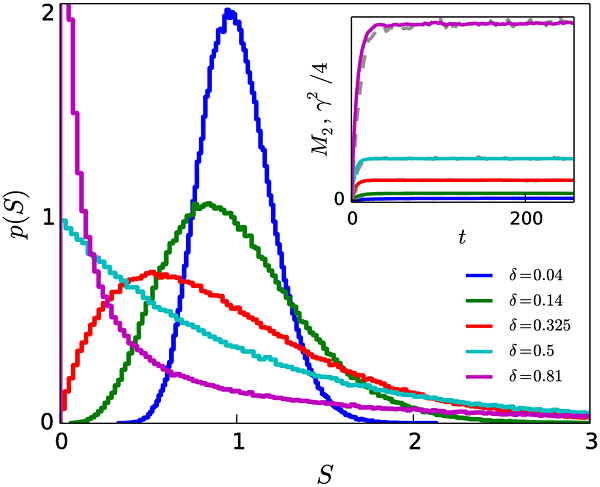
To do so, we construct a generalized winner-loser model in which we intend the strength property to represent societal status. The amount of status gained by the winner and lost by the loser of each fight is proportional to the pre-fight status of the losing individual. We define a probability for winning that is determined by the relative statuses of the two competitors, modulated by a parameter spanning a continuous range of degree of authoritarianism from redistributive (lower-status opponent always wins) to totalitarian (higher-status opponent always wins). The latter modulation for winning contains previous models as special cases at specific values of the authoritarianism parameter, and allows a more general description of the dynamics. Over a large range of parameters and excluding these special cases, we find the emergence of long-lived intermediary societal structures (distributions of societal status) for the first time. Establishing the existence of these long-lived structures—which can give the illusion of a stable society—and the relationship between the characteristic time of their evolution and the model parameters is one of the main contributions of our study.
To demonstrate the relevance of our generalized model and the long-lived structures, we analyze real-world data. Specifically, we compare data from observational studies on wins and losses in animal interactions with the results from simulations of our model, and we compare the distributions of societal status produced by the model with real-world social hierarchies. To make the latter comparison, we use proxies for societal status in large social groups. In both cases, the real-world data are consistent with our model. Specifically, in our model, long-lived intermediary societal structures (distributions of societal status) arise independent of whether any pair of individuals are equally likely to interact or not. In the latter case, however, status distributions with more complex shapes consistent with the household income proxy emerge. We are able to fit the simulated status distributions to USA household income data with good agreement. To our knowledge, this is the first model that produces the two-part structure of the proxy distribution by self-organization based solely on interacting individuals.
The model is presented in section 2 and an extended version of it in which similar-status individuals interact more frequently than individuals with large differences in status is presented in section 2.1. Details about the shapes of the status distributions and their evolution in time are presented in section 3. Comparison of model results to data from real societies is contained in section 4, where we consider data on agonistic interactions in non-human animals in section 4.1 and proxies for societal status in large social groups (social insects and humans) in section 4.2. The article concludes with a summary of results and some comments regarding future research directions.
2 Definition of the model
Winner-loser models have been constructed using many variations of the rule determining who wins the fight and the rule determining the amount of strength gained or lost in a fight, where the particular formulation chosen for each rule depends on the system under study.
In the rule determining the amount of strength gained and lost in a fight, two formulations have been applied previously. In one version (“additive” rule), the effect of fighting on an individual’s strength accumulates additively, for example, by the addition or subtraction of a fixed increment of status [20–25]. In an additive rule, the amount of strength gained or lost in a fight does not depend on the current value of either individual’s strength. This means that the amount of strength won or lost in a fight is always the same, regardless of the strength of one’s opponent.
The other version of this model rule is a “multiplicative” one. Here, the amount of strength gained or lost is proportional to the strength of one of the individuals involved in the fight, such that effect of fighting accumulates multiplicatively [27, 31–33]. Defeating a strong opponent produces a large increase in strength, whereas defeating a weak opponent produces a small increase in strength. It is clear from animal behaviour studies that wins against high ranking individuals increase the rank of an individual more than wins against low ranking individuals. In this case, a multiplicative rule is therefore more realistic than an additive rule, in which it is no more advantageous for an individual to defeat a strong rather than a weak rival. Moreover, whether an additive or multiplicative rule is used leads to substantially different distributions of strength [19]. For example, in many models with additive rules, strength becomes distributed such that individuals of adjacent ranks are separated by the same amount of strength. In multiplicative models, on the other hand, highly skewed distributions can result, and such multiplicative processes have been proposed as a common underlying cause of observed inequalities in natural and social systems [35, 36].
Here, we implement a formulation of the multiplicative rule in which the amount of strength won or lost is proportional to the pre-fight status of the losing individual (“loser scheme”). In another formulation that has been used in several econophysics models [32–34, 37–39], the amount of strength won or lost is proportional to the pre-fight status of the weaker individual, regardless of who wins or loses (“poorer scheme”). The loser scheme formulation is more realistic in the context of dominance hierarchies, because upset victories, in which the lower-strength individual in the pair wins, produce large rewards for the winner and large penalties for the loser. For example, in primate dominance hierarchies, only a small number of repeated defeats of a higher-strength individual by the same lower-strength individual are required for their rankings to be reversed [40]. This scenario is captured by the loser scheme but not by the poorer scheme.
With regards to the rule determining which individual wins in a pairwise fight, two primary formulations have been applied: one in which the probability that the stronger individual wins depends on the difference in the strengths of the two individuals [20–23, 26, 33], and one in which this probability depends on a ratio of the strengths of the two individuals [27–29]. We focus on the latter of these two formulations. This choice is related to our choice of the multiplicative rule for the amount of strength won or lost in the fight. In a multiplicative rule, large absolute differences in strength typically exist among individuals of similar rank, at the top-end of the strength distribution. Therefore upsets, in which the lower-strength individual defeats the higher-strength individual, become very unlikely or impossible at the top-end of the distribution of strength when the probability of winning depends on the difference in strengths of the two individuals. When the probability of winning depends on a ratio of the statuses of the two individuals, upsets tend to be more likely, especially between two high-strength individuals separated by a large absolute amount of strength.
Conversely, in a model with an additive rule for the amount of strength won or lost, it may well be appropriate for the probability of winning to depend on the difference in strengths of the two individuals, since the status of an individual is equal to the difference in the number of times the individual has won and lost fights. However, especially in more complex animals, it is unrealistic to assume that the probability of winning is based on a tally of the number of fights won and lost, as this information is unavailable to the individuals involved in the fight. Rather, a more realistic assumption is that a psychological process occurs in which the two individuals make a rough comparison of one another’s relative strengths, where this comparison influences each individual’s probability of winning via characteristics such as confidence, willingness to take risks, and aggressiveness [2, 27]. This assumption is supported by psychological research showing that perceived change of a physical stimulus depends on the relative rather than the absolute change in the stimulus [19, 41].
Our specific model is constructed as follows. We consider a system of N individuals, each possessing a strength property, S, that determines the individual’s societal position. We intend S to represent the societal status of the individual, and accordingly we refer to “status” rather than the generic term “strength” in the remainder of this article. At each step in the simulation, a pair of individuals is randomly selected, and engages in a “fight”. The probability, p, that the higher-status individual wins the fight is expressed as a function of its status, S1, and that of its (lower or equal status) opponent, S2:![]()